Algunas curiosidades
sobre el número Pi ( ) ) |
- Pi es la razón de la circunferencia de un circulo a
su diámetro
- En distintas culturas, china, egipcia, europea,
india, etc., se trato de obtener mejores aproximaciones de Pi por ser de
aplicación en campos tan distintos como la astronomía o la construcción.
- Muchos de los intentos de evaluar Pi en la antigüedad
utilizaban el método de calcular el perímetro de polígonos inscritos y
circunscritos a circunferencias.
- Modernamente para evaluar Pi se utiliza una serie
infinita convergente. Este método fue utilizado por primera vez en Kerala
(India) en el Siglo XV
- La probabilidad de que dos enteros positivos
escogidos al azar sean primos entre si es 6/Pi2
- Si se eligen al azar dos números positivos menores
que 1, la probabilidad de que junto con el número 1 puedan ser los lados
de un triángulo obtusángulo es (Pi-2)/4
- En 1706, el inglés William Jones fue el
primero en utilizar el símbolo griego
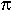 para denotar la relación entre la circunferencia y su diámetro. Euler
en su obra "Introducción al cálculo infinitesimal", publicada
en 1748, le dio el espaldarazo definitivo.
para denotar la relación entre la circunferencia y su diámetro. Euler
en su obra "Introducción al cálculo infinitesimal", publicada
en 1748, le dio el espaldarazo definitivo.
- Muchos intentos para determinar Pi con exactitud están
relacionados con el clásico problema de la cuadratura del círculo :
"construir, utilizando únicamente regla y compás, un cuadrado de área
igual a un círculo dado".
- Johan Heinrich Lambert(1728-1777), matemático
alemán, probó que Pi es irracional. ( Un número irracional no se puede
escribir en forma de fracción racional. Números racionales son : 1, 2 ,
3/4, 17/23)
- Ferdinand Lindemann(1852-1939) demostró que
Pi es un número trascendental. Esto significa entre otras cosas que el
problema de la cuadratura del círculo no tiene solución. Pese a ello
todavía se sigue intentando.
Algunos valores de Pi obtenidos antes de 1600
| Matemático o Lugar |
año |
valor |
| La Biblia (Reyes-I-7-23) |
|
3 |
| Papiro de Ahmes (Egipto) |
1650 a.C. |
3,16 |
| Tablilla de Susa (Babilonia) |
1600 a.C. |
3,125 |
| Bandhayana (India) |
500 a.C. |
3,09 |
| Arquímedes de Siracusa |
(287-212 a.C) |
entre 223/71 y 220/70 |
| Liu Hui (China) |
260 |
3,1416 |
| Tsu Chung Chih |
480 |
Entre : 3,145926 y 3,1415927 |
| Al-Kashi (Persia) |
1429 |
3,1415926535897932 |
| Franciscus Vieta (Francia) |
(1540-1603) |
3,1415926536 |
- El matemático alemán Ludolph van Ceulen(1540-1610)
pidió que, como epitafio, escribiesen en su lápida las 35 cifras del número
Pi que había calculado. Los alemanes llaman a Pi el número ludofiano.
- William Shanks, matemático inglés, dedico 20
años de su vida a la obtención de 707 decimales de Pi.(En 1945 se
descubrió que había cometido un error en el decimal 528 y a partir de
este todos los demás eran incorrectos)
- En 1949 uno de los primeros ordenadores el ENIAC,
trabajando durante 70 horas, determino Pi con 2037 decimales.
- En 1959, ordenadores en Francia e Inglaterra
calcularon más de 10.000 cifras de Pi.
- En 1961 Daniell Shanks(sin relación con
William Shanks) y Wrench, obtuvieron en 8 h 23 min, 100.265 cifras
en un IBM 7090.
- En 1983, Yoshiaki Tamura y Yasumasa Kanada,
en menos de 30 h, en un HITAC M-280 H obtuvieron 16.777.206 (224)
cifras.
- En Julio de 1997, Yasumasa Kanada y Daisuke
Takahashi obtuvieron 51.539.600.000 cifras , utilizando un HITACHI
SR2201 con 1024 procesadores.
- Programas para simular el problema de la
aguja de Buffon: Buffon (DOS) (9 kbytes),
Buffon (Windows 95)(143 kbytes)
- Super Pi for Windows
(Ver 1.1, Windows 3.1, 72 kbytes) hecho por el equipo de Kanada
& Takahashi, te permite calcular pi con 33.55 millones de dígitos.
- Si quieres conocer unas cuantas cifras
de Pi
- Busca
tu número de teléfono en las 50.000.000 primeras cifras de Pi
- Página
de enlaces sobre Pi (en inglés)
- Simon Newcomb, astrónomo y matemático
americano, dijo en una ocasión que treinta cifras decimales de Pi darían
la circunferencia del universo visible hasta una cantidad que sería
imperceptible incluso con el más potente telescopio.
|